Physical Simulation: Rayleigh-Bénard Convection
March, 2019
In Collaboration with Michael S. Emanuel and Jonathan Guillotte-Blouin

This project uses Drekar and simulates a 2D turbulent Rayleigh-Bénard Convection using 512 and 1024 CPU cores on Harvard’s Odyssey supercomputinng cluster. Postprocess includes temperature fields, velocity streamlines and Schlieren flow visualizations. Click here to view full visualization including velocity and pressure fields. (C++)
Physical Simulation: Fluid Maze Solver
October, 2019
This is a side-project of my master’s thesis. It simulates using fluid to solve a maze based on the lattice Boltzmann method. More details will be added later. (C++)
Computer Graphics: Starry Waters, A Moving Van Gogh
December, 2018
In Collaboration with Claudia Wu
The motivation for this project was to reinterpret classical art pieces using modern digital techniques and bring them to life. It was inspired by the movie “Loving Vincent” and Maciek Janicki’s “The Life of Van Gogh”. Specifically, this project to recreate Van Gogh’s painting “The Starry Night Over the Rhone” and imbue it with movement. To accomplish the final result, three techniques were implemented: painterly render, refraction and water height field. (C++, OpenGL)
Physical Simulation: Simulation of A Droplet in Water
December, 2018
Multiphase flow are quite common in our daily life. For example, oil droplets in water and milk in coffee are both examples of multiphase flow. The patterns generated by adding one fluid into another are unexpected, but always beautiful. The motivation of the project was to model the phenomenon of adding milk into coffee, and simulate the pattern generated by such process. To simplify the model and decrease the computational difficulties, the project limited the number of droplet to be one and the shape to be circles only. Also the two fluids were assumed to be incompressible and have the same viscosity. This project mainly implemented the finite volume method following LeVeque’s textbook and the front-tracking method introduced by Gretar Tryggvason. (Python)
Software Development: DeriveAlive, An Autodifferentiation Package
December, 2018
In Collaboration with Stephen Slater and Chen Shi
GitHub: https://github.com/cs207-group19/cs207-FinalProject
Documentation: https://cs-207-final-project-group-19.readthedocs.io/en/latest/
PyPI: https://pypi.org/project/DeriveAlive/#files
This is a package for autodifferentiation. It includes several additional features making use of autodifferentiation, including root-finding, optimization (gradient descent, BFGS, and dataset compatability for optimizing mean squared error), and quadratic spline fitting. There is extensive documentation at the link below, and the project is publicly available for download via PyPI by running pip install DeriveAlive. (Python)
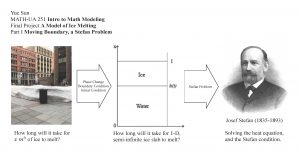
Physical Simulation: A Model of Ice Melting
May, 2017
This project constructs a model for one-dimensional ice melting process, and numerically simulates the melting time of certain length of ice slab under different melting temperatures. The model involves solving the heat equation with a moving boundary condition, hence we study the Stefan problem, i.e. the moving boundary condition problem. This project solves both analytically and numerically for this one-dimensional heat equation with moving boundary condition. (MATLAB)
(Presentation for the final results⬇️)